Python基础算法解析：逻辑回归

逻辑回归是一种常用的分类算法，尤其适用于二分类问题。本文将介绍逻辑回归的原理、实现步骤以及如何使用Python进行逻辑回归的编程实践。

什么是逻辑回归？

逻辑回归是一种基于概率的统计分类技术，主要用于二分类问题。尽管名字中含有“回归”，但实质上是一种分类算法。逻辑回归通过将特征值的线性组合传递给一个称为sigmoid函数的激活函数，将线性输出转换为概率输出，从而进行分类。

逻辑回归的原理

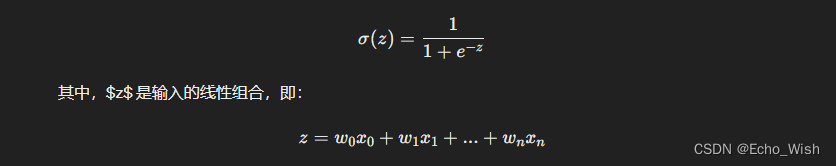
逻辑回归的核心在于 sigmoid 函数，它的数学表达式如下：

这里，$x_0 = 1$，$w_i$ 是特征 $x_i$ 对应的权重。sigmoid 函数将 $z$ 映射到 0 到 1 之间，表示样本属于正类的概率。

逻辑回归的实现步骤

数据预处理：包括数据清洗、特征选择、特征缩放等。
参数初始化：初始化权重 $w$ 和偏置 $b$。
定义sigmoid函数：将线性输出转换为概率输出。
定义损失函数：使用对数损失函数来衡量模型的拟合程度。
梯度下降优化：利用梯度下降算法更新模型参数，使损失函数最小化。
预测：根据模型输出的概率值进行分类预测。

Python实现逻辑回归

下面我们通过Python代码来演示如何实现逻辑回归：

import numpy as np

class LogisticRegression:
    def __init__(self, learning_rate=0.01, num_iterations=1000):
        self.learning_rate = learning_rate
        self.num_iterations = num_iterations
        self.weights = None
        self.bias = None

    def sigmoid(self, z):
        return 1 / (1 + np.exp(-z))

    def initialize_parameters(self, n_features):
        self.weights = np.zeros(n_features)
        self.bias = 0

    def fit(self, X, y):
        n_samples, n_features = X.shape
        self.initialize_parameters(n_features)

        for _ in range(self.num_iterations):
            linear_model = np.dot(X, self.weights) + self.bias
            y_predicted = self.sigmoid(linear_model)

            dw = (1 / n_samples) * np.dot(X.T, (y_predicted - y))
            db = (1 / n_samples) * np.sum(y_predicted - y)

            self.weights -= self.learning_rate * dw
            self.bias -= self.learning_rate * db

    def predict(self, X):
        linear_model = np.dot(X, self.weights) + self.bias
        y_predicted = self.sigmoid(linear_model)
        y_predicted_cls = [1 if i > 0.5 else 0 for i in y_predicted]
        return y_predicted_cls

在上述代码中，我们定义了一个名为LogisticRegression的类，包括了初始化参数、sigmoid函数、参数初始化、拟合、预测等方法。其中，fit方法用于拟合模型，predict方法用于进行预测。

使用逻辑回归进行分类

现在，让我们使用逻辑回归模型对一个简单的数据集进行分类：

from sklearn.datasets import make_classification
from sklearn.model_selection import train_test_split
from sklearn.preprocessing import StandardScaler

# 生成一个二分类数据集
X, y = make_classification(n_samples=1000, n_features=20, n_classes=2, random_state=42)

# 数据集划分为训练集和测试集
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=42)

# 特征缩放
scaler = StandardScaler()
X_train = scaler.fit_transform(X_train)
X_test = scaler.transform(X_test)

# 训练模型
model = LogisticRegression(learning_rate=0.01, num_iterations=1000)
model.fit(X_train, y_train)

# 预测
y_pred = model.predict(X_test)

# 计算准确率
accuracy = np.mean(y_pred == y_test)
print("Accuracy:", accuracy)

总结

逻辑回归是一种简单而强大的分类算法，在许多实际应用中都表现出色。通过本文的介绍，你已经了解了逻辑回归的原理、实现步骤以及如何使用Python进行编程实践。希望本文能够帮助你更好地理解和应用逻辑回归算法。

发送评论编辑评论